 Fig0.The
dome and the bridge in Park Hanamizuki in Japan
Fig0.The
dome and the bridge in Park Hanamizuki in Japan
Katsuhito Atake
ATAKE Space Design Laboratory Co., Ltd. Japan
Abstract
This presentation propose a new kind of a scissors technique which is a framework structure comprises three or more primary constituent units each including two rigid diagonal members constituting the diagonals of a quadrangular lateral face of a solid and coupled together for relative rotation about a first rotation axis passing through the intersection of the diagonals. The primary constituent units are coupled to one another via second and third rotation axes into a ring-like form. A more complicated framework structure can be obtained by using a plurality of these framework structures as secondary constituent units which are coupled to one another with a coupler or a primary constituent unit (scissors) used in common between adjacent ones of the secondary constituent units .
Using complete pin joints composed by three axis in between scissors makes the system more flexible and it makes almost all kind of 3D-shapes folding into bundle. Adding tension component like wire or membranes to its developed form, it becomes 3D-truss and gets effective strength.
We think this method is useful for rapid construction of towers bridges domes and space structures.
 Fig0.The
dome and the bridge in Park Hanamizuki in Japan
Fig0.The
dome and the bridge in Park Hanamizuki in Japan
1 The principle - simple ring
The minimum component of this system is so called scissors which define two diagonal lines of a quadrilateral and which are pivotally connected to each other at a point of intersection. At least three minimum component connected to one another to form a ring through complete pin joints which has three axis (ordinary door hinge could use for it), provide a secondary unit of this frame structure. And in order to make 3d-variable structures, at least the quadrilaterals from which diagonal frames are taken out must be trapeziums in mathematics.
1.1 Application to frustum of pyramid
These simple ring can be divided mainly two types. One is based on frustum of pyramid type. We call these type of secondary unit simply pyramid type. Only triangular pyramid is stable when tension components are added.
 Fig 1.1.1
triangular pyramid unit
Fig 1.1.1
triangular pyramid unit
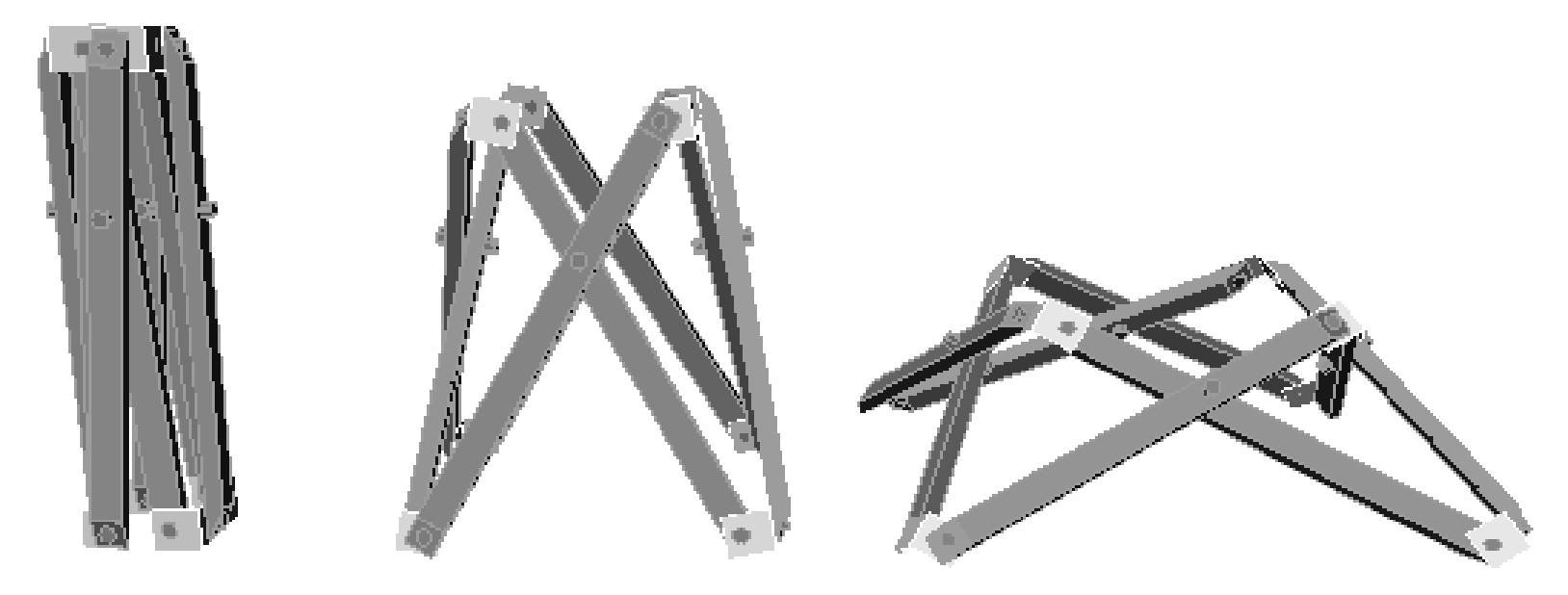 Fig 1.1.2
square pyramid unit
Fig 1.1.2
square pyramid unit
 Fig 1.1.3
pentagonal pyramid unit
Fig 1.1.3
pentagonal pyramid unit
1.2 Application to sliced skew prism
When the number of scissors in one ring is even, there
is another type of ring which is almost stable solutions.
It is based on sliced skew prism. We call this type simply
skew type.
When the number is 4 ,the skew will be tetrahedron. And
when the number is 6 , the triangular skew prism will be octahedron.
To combine these two types of unit can provide more complicate
foldable structures.
 Fig 1.2.1
minimum skew type based on sliced tetrahedron
Fig 1.2.1
minimum skew type based on sliced tetrahedron
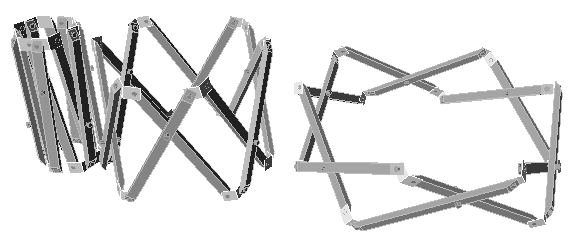 Fig 1.2.2
skew type based on sliced octahedron
Fig 1.2.2
skew type based on sliced octahedron
3 Vertical connection of ring units
3.1 Application to towers
Piling up these pyramid type structural unit vertically
it becomes an foldable tower.
If the reduction ratio of units are geometrical this
tower can transform into completely plane.
To use this method we can make high tower without working
in high place.




 Fig3.1 Tower Model the maximum height is about 2600mm
Fig3.1 Tower Model the maximum height is about 2600mm
3.2 application to bridges
Applying this vertical connection to horizontal like a balancing toy, it becomes foldable bridge easy to construct. It will be useful for rapid construction of a fly over or a bridge for pedestrians. The Bridge of Hanamizuki Park-Fig0. is designed for this method. But actuary it was not constructed by this way .
Fig 3.2 shows an other project applied to suspension type of bridge and the developing. The bridge is designed that to pull the suspension wire make it develop.
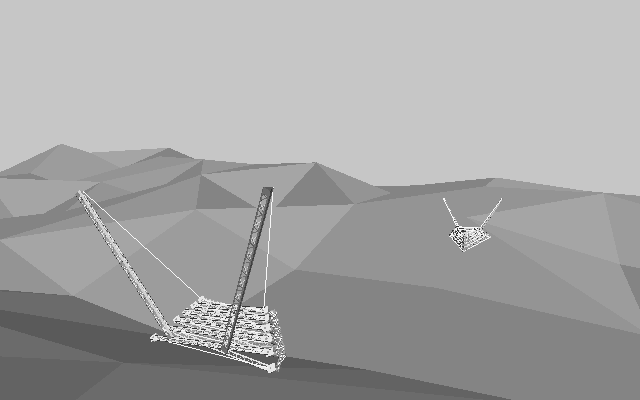
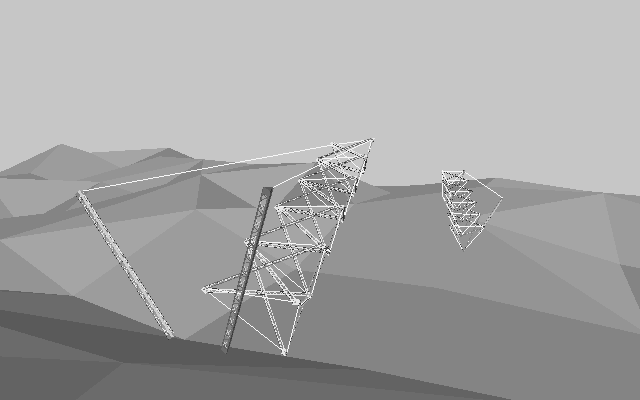

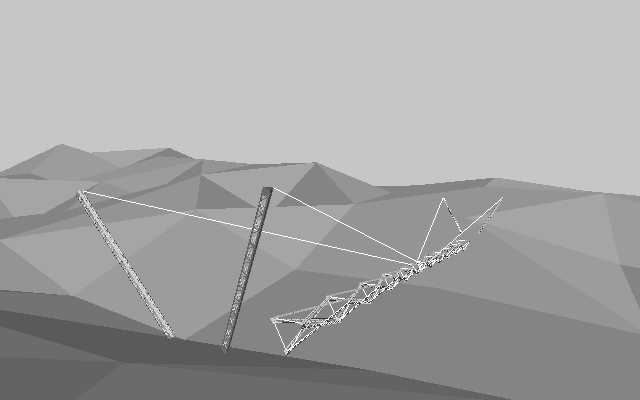
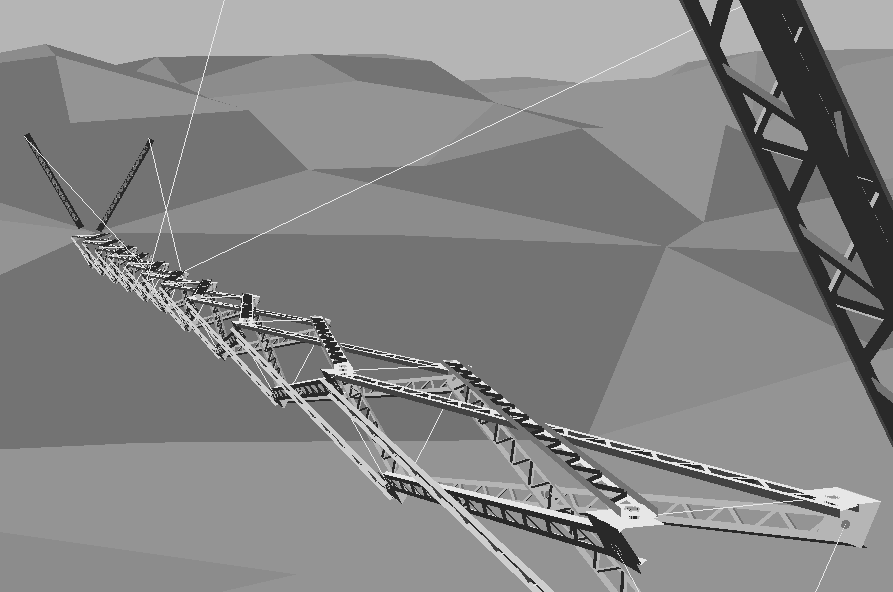
Fig3.2 A suspension bridge project the span is 50m
3 Horizontal connection of secondary units
To connect secondary unit horizontally by scissors in common compose various 3d foldable shapes.
3.1 Application to double layer polyhedron
To connect only pyramid type unit horizontally compose
double layer polyhedron.
All kind of regular and semi regular polyhedron can obtain
by this method. But most of them are not stable.
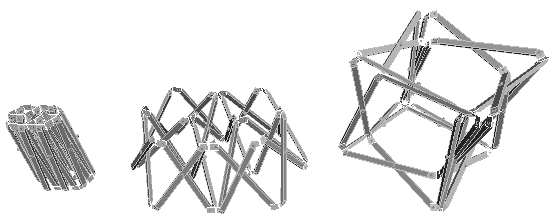 fig.3.1
double layer cube - this is not stable itself.
fig.3.1
double layer cube - this is not stable itself.
3.2 Application to chairs
Horizontal connection of only skew type unit compose complex shapes like chairs. The liner connection compose simple arch and most of them are stable.
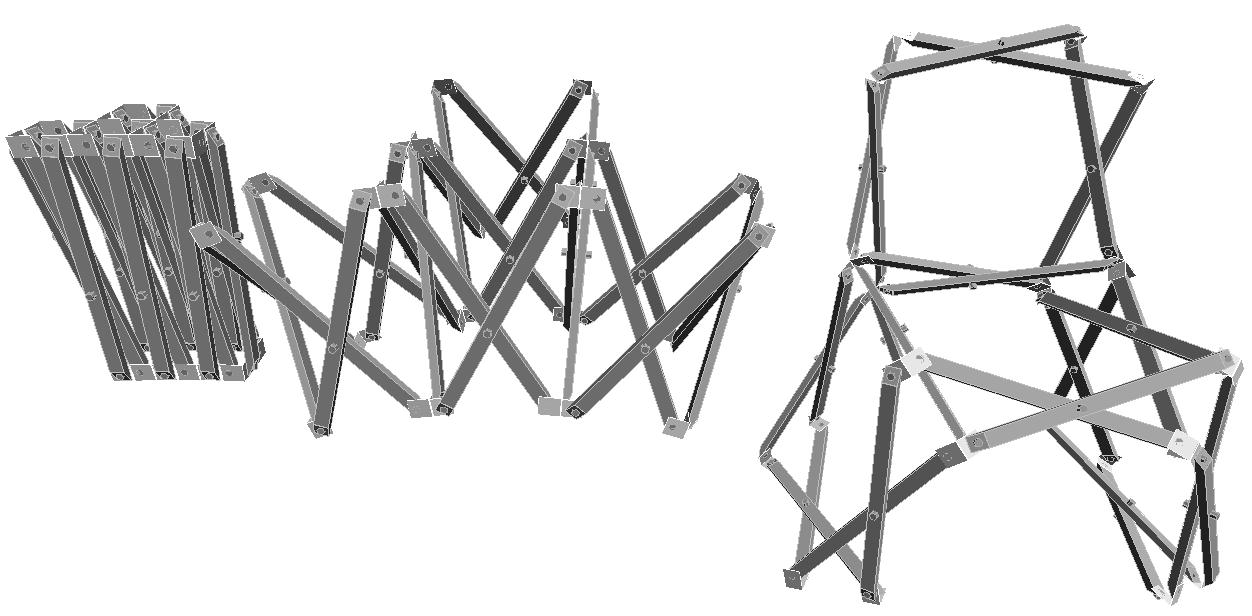 fig.3.2.1
foldable chair - this is almost stable
fig.3.2.1
foldable chair - this is almost stable
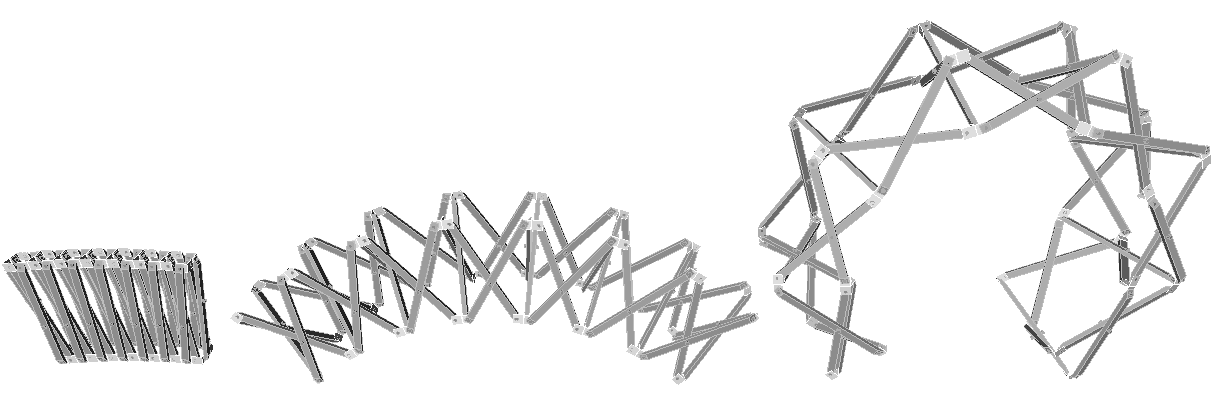
fig.3.2.2 foldable arch
3.3 Application to double layer plates
In case of the number of components in one unit is four, two type of shape the pyramids and the sliced skew prism are complemented to each other. It is according to a space packing pattern of octahedral and tetrahedral.
So it is considerable to apply this system to the octet truss (space truss) system double layer truss plate based on square.
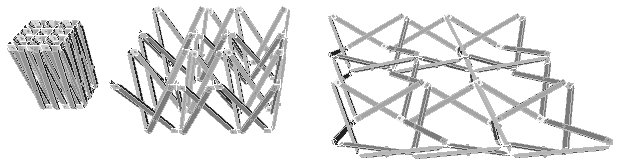 Fig 3.3.1
square plate
Fig 3.3.1
square plate
Octet truss based on triangular or hexagonal plate structure
is also realize to use this system.
Here are frustum of triangular pyramid and sliced octahedral
complementary.
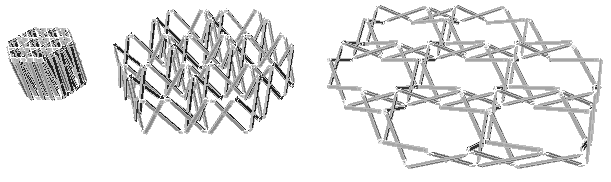 Fig 3.3.2.
hexagonal plate
Fig 3.3.2.
hexagonal plate
3.4 Application to vaults
Lateral connection of arches by inverted scissors or pyramid
units provide foldable double layer vault.
These vault can get more complex curve to change the
dividing ratio of each scissors.
 Fig
3.4 double layer vault
Fig
3.4 double layer vault
3.5 application to domes
horizontal connection of sliced octahedron unit applied to the hexagon of upper half of semi regular 32 polyhedron (soccer ball) provide foldable double layer domes. It is a kind of fuller domes. This is composed by all same 48 scissors and almost stable itself.






Photos below shows the development of the dome in Park
Hanamizuki
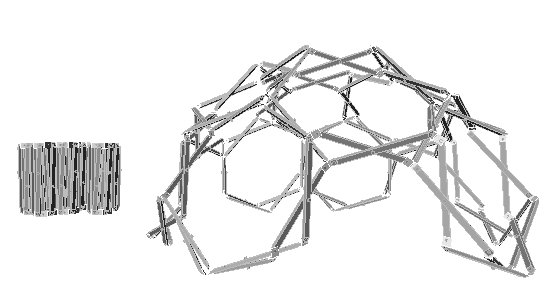 fig.3.5 double
layer dome
fig.3.5 double
layer dome
3.6 Application to boats




 Two inverted triangular pyramid connected skew composed boat shape. This
structure can provide foldable boat.
Two inverted triangular pyramid connected skew composed boat shape. This
structure can provide foldable boat.
 Fig 3.6 Folding
boat
Fig 3.6 Folding
boat
4. Plan Diagram
It is difficult to express and to understand these structures
through real 3D graphics, but when the structure is fold up, the shape
is almost same except the end (the top view),so only the symbolic diagram
of top view could express hole structure. figure 3 shows the relation the
diagram and 3D shape. The length of the line shows the length of bottoms
of the trapezoid .
To construct the units as the fold up shape by this diagram
is not so hard. And the final shape can be obtained to expand the unit.

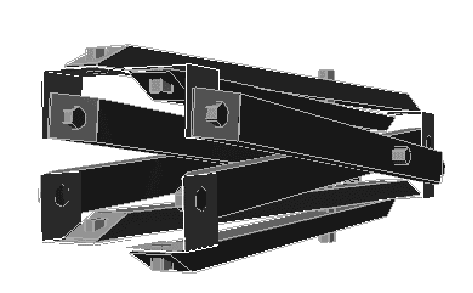
Fig 4.1 Plan diagram of inverted pyramid (left) and skew (right)
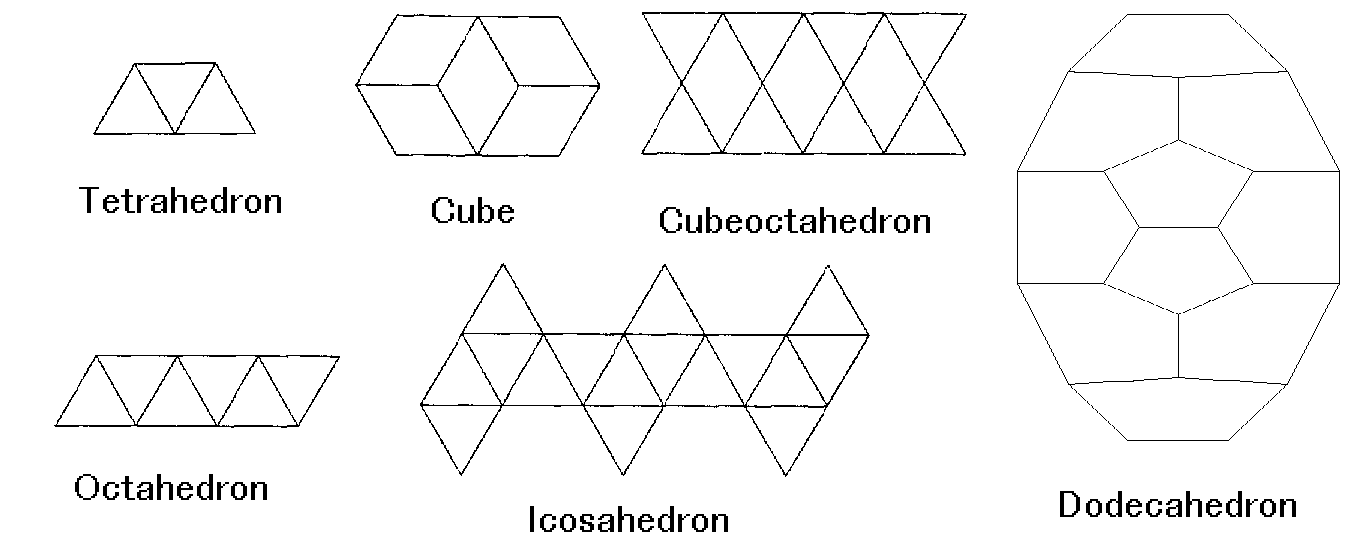 Fig4.2 Plan
diagram of polyhedron -all units are pyramid type
Fig4.2 Plan
diagram of polyhedron -all units are pyramid type
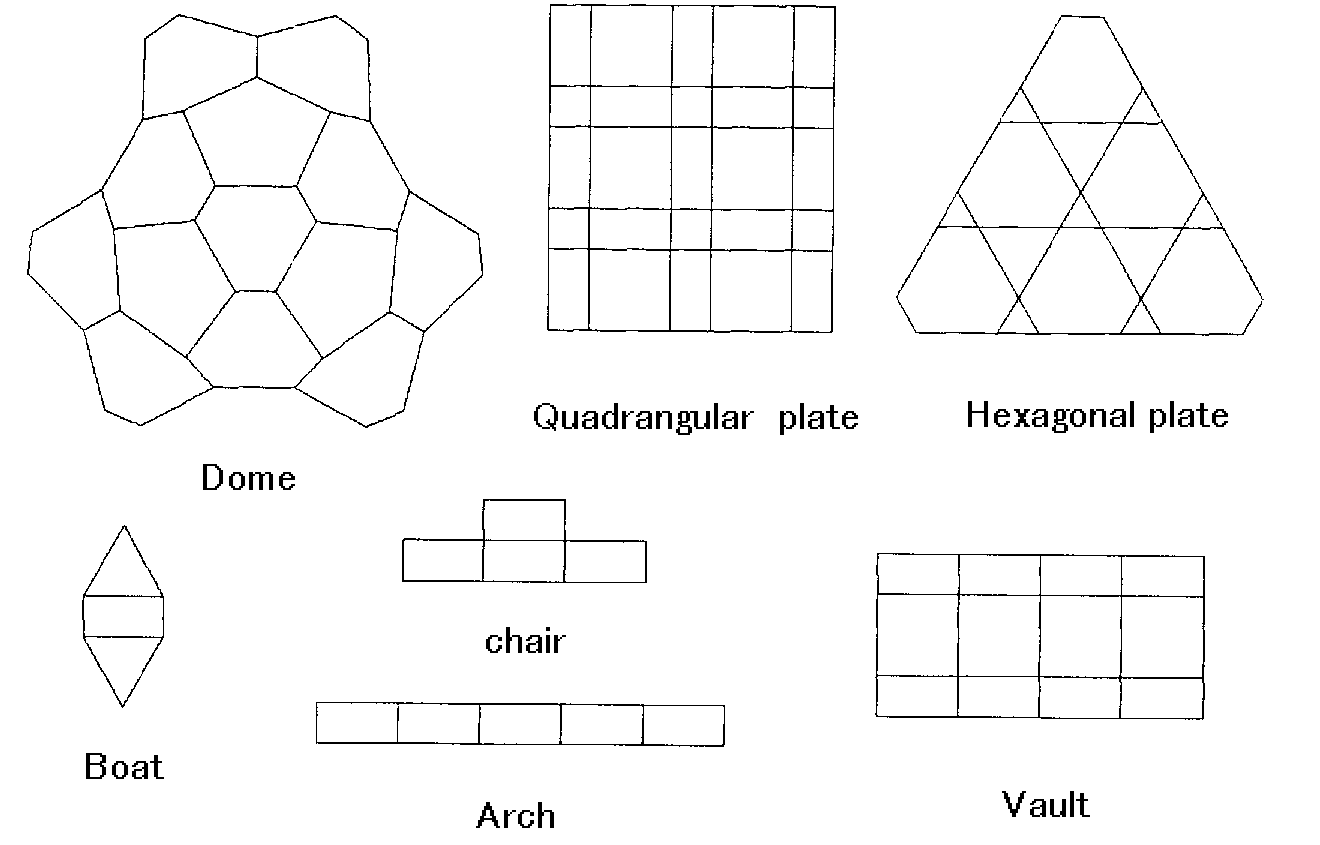 Fig4.3 Plan
diagram of various shapes -units are combined
Fig4.3 Plan
diagram of various shapes -units are combined
References
Katachi U Symmetry Extended Abstract university of Tukuba
pp345-348 1994
Symmetry Culture and Science Extended Abstracts 1 ISIS Symmetry
pp53-56 vol1 1995
[3]http://www.atake-sdl.com/
[4]http://www.ne.jp/asahi/gallery/atake/